最近在学$LCA$算法的时候发现了很有意思的一个方法:
建树,利用$LCA$解决$RMQ$问题。
现在就来讲讲$RMQ$问题的$LCA$解决。
先来个例子:
已知序列A={2,8,5,7,1,4},求区间[l,r]之间的最小值。
- 第一步:建立树$T$
我们把全局最小值$1$作为根节点,建立一棵优先级树。
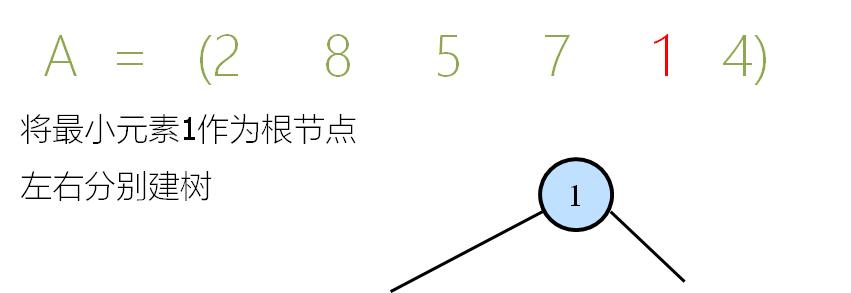
接下来,我们建立右子树,但$1$右侧只有一个结点可建:$4$
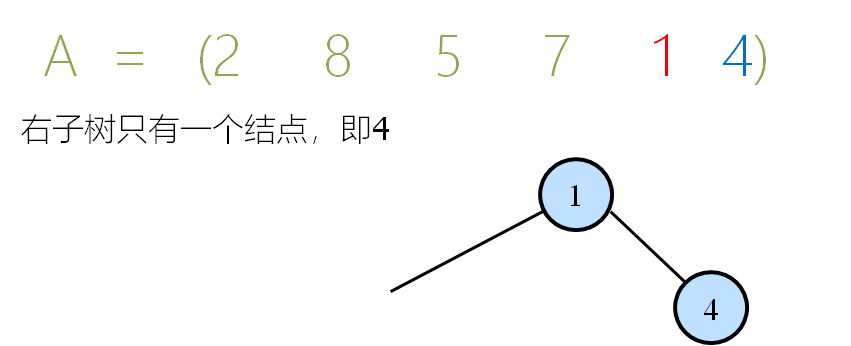
下一步建立左子树,左子树有$4$个结点可建:$2,8,5,7$
我们选择最小的$2$作为子树根结点建树
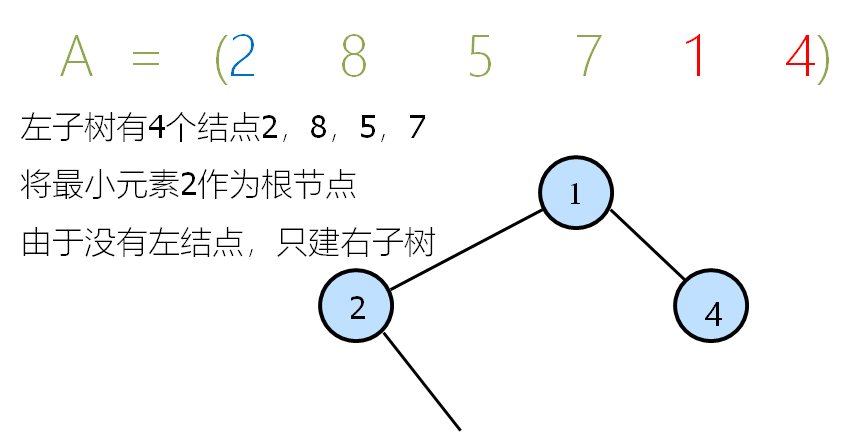
下面递归建树即可:
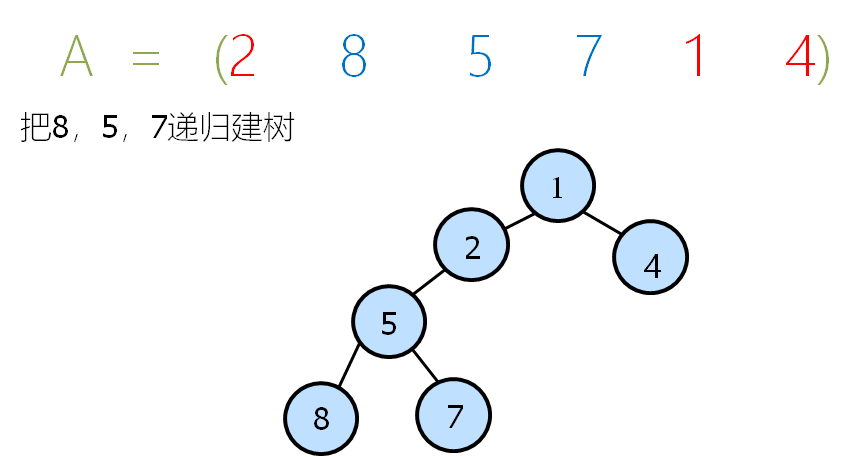
- 第二步:$LCA$
现在我们已经把序列$A$转换为了一棵优先级树,那么现在我们可以发现:$RMQ$问题已经转化为了求$LCA$。
比如:求 序列中值为$7$和$4$的元素之间的区间的最小值。
找一次$LCA$:$7,4$拥有最近公共祖先$1$,那么RMQ就是$1!!$
回顾一下解决过程:
- 考察一个长度为$N$的序列$A$,按照如下方法将其递归建立为一棵树:
- 设序列中最小值为$A_k$,建立优先级为$A_k$的根节点$T_k$;
- 将$A_{1…k-1}$递归建树作为$T_k$的左子树;
- 将$A_{k+1…N}$递归建树作为$T_k$的右子树;
- 这棵树是一棵优先级树
那么……
对于$RMQ$($A,i,j$):
设序列中最小值为$Ak$,若$k∈$[$i, j$],那么答案为$k$;
若$k > j$,那么答案为$RMQ$($A_{1..k-1},i,j$);
若$k < i$,那么答案为$RMQ$($A_{k+1..N},i,j$);
不难发现$RMQ$($A,i,j$) $=$ $LCA$($T,i,j$)!
- 这就证明了$RMQ$问题可以转化为$LCA$问题。
那么继续思考:$LCA$问题可不可以转化为$RMQ$?
答案是肯定的。
如果对有根树$T$进行$DFS$,将遍历到的结点按照$DFS$序记下,我们将得到一个长度为$2N-1$的序列,称之为$T$的欧拉序列$F$
每个结点都在欧拉序列中出现,记录结点$u$在欧拉序列中第一次出现的位置为$pos_u$
就比如说这样(版权所有:$first_fan$)

那么我们就可以得到欧拉序列$F$,深度序列$B$,以及首次出现位置$pos_u$
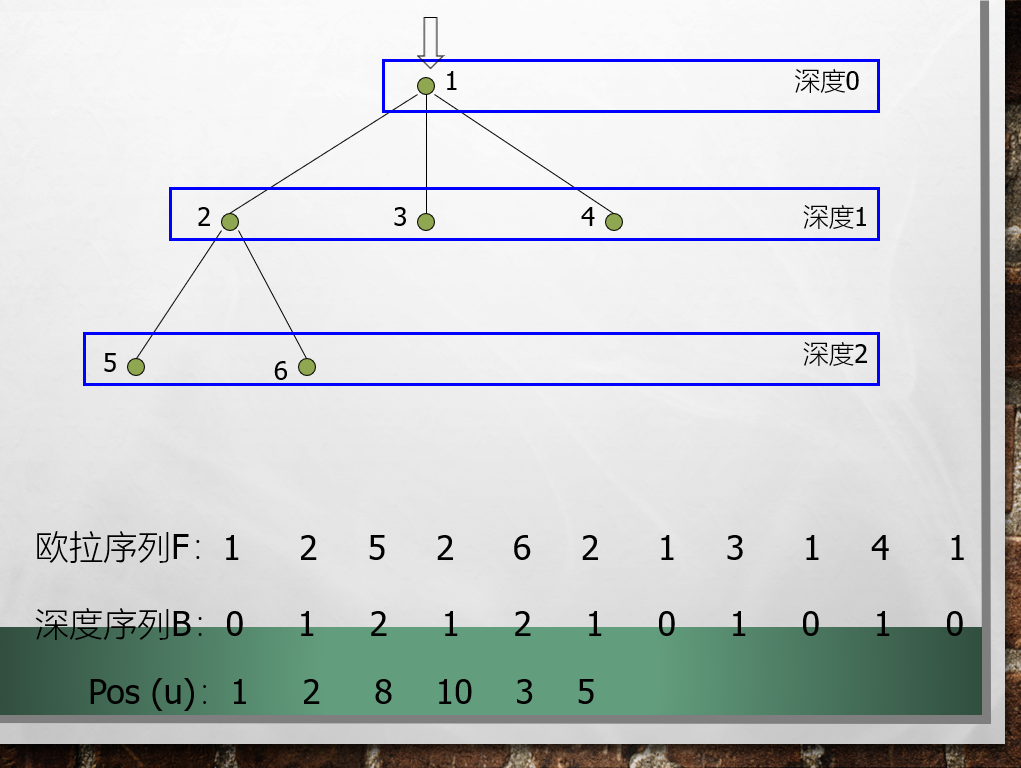
那么怎么转化为$RMQ?$
根据$DFS$的性质,对于两结点$u,v$,从$pos_u$遍历到$pos_v$的过程中经过$LCA(u, v)$有且仅有一次,且深度是深度序列$B[pos_u…pos_v]$中最小的
即$LCA(T, u, v)=RMQ(B, pos_u, pos_v)$【$O(N)$】
那么有$LCA$&$RMQ$可以$O(N)$内互相转化
得到:一般$RMQ$问题可以$ST$表解决,并且在$O(n)$可以与利用$Tarjan$算法的$LCA$问题互相转化。
例题:($WC_{2006}$)LuoGu4172:水管局长
题目的模型翻译过来就是:
定义一个路径的关键边为其边权最大的边;
定义一个路径的权值为其关键边权值;
定义两点之间最短路为所有路径中权值最小的一条;
两种操作:拆除无向边&询问最短路
这个问题的解决,我们需要引入最小生成森林以及$Kruskal$生成顺序森林的算法,详情请参考:
即将完成的图论史诗板块