想必来到这篇文章的人都知道汉诺塔是什么:
三根柱子,一摞盘子,小盘在大盘上,挪到目标柱上。
如图:

这是学习语言理解递归最最基本的一个程序。
想想正常的做法:
视角换至最底层盘,则要把所有上面的盘移动至无关盘上。
随后把最底层盘挪至目标处,转换为少一个盘的相同问题。
重复上述操作,直到只剩1个,放到目标盘即可。
典型的递归思路。
但我接下来要说的是它与二进制数的关系
我在玩汉诺塔时,发现一个很有意思的现象:
如果你用二进制数记录你每次的挪动的话,就会像这样:(从上至下依次编号$1-n$)
- 未挪动时
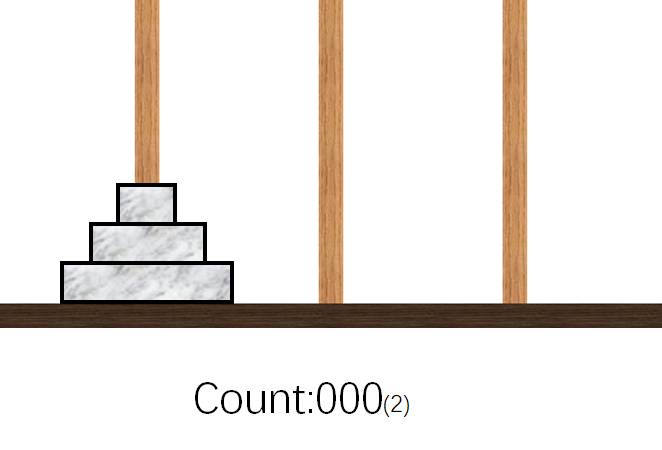
- 挪动$1$号盘至$C$柱
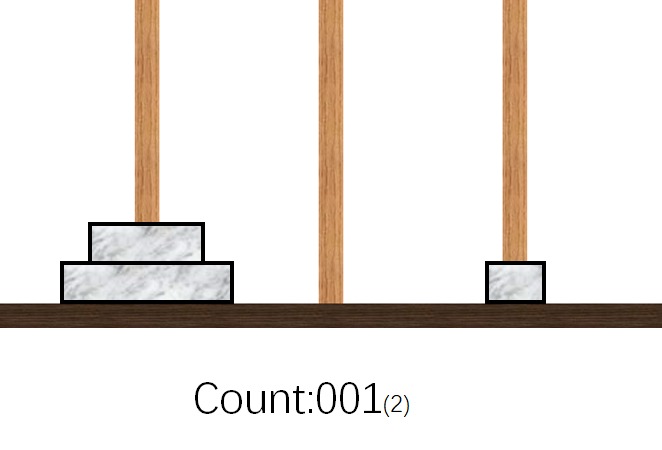
- 挪动$2$号盘到$B$柱
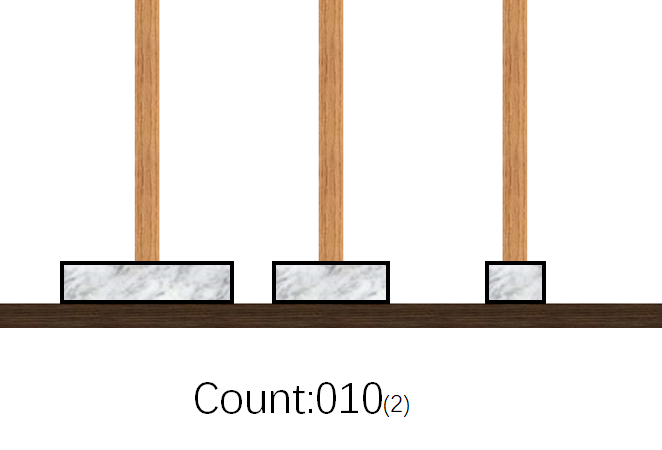
- 挪动$1$号盘到$B$柱
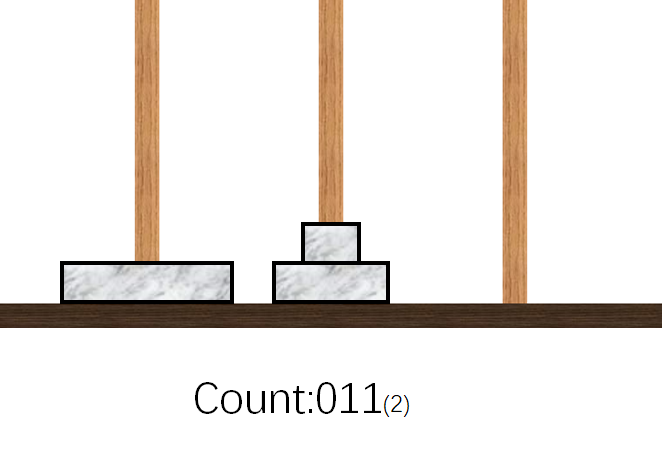
- 挪动$3$号盘到$C$柱
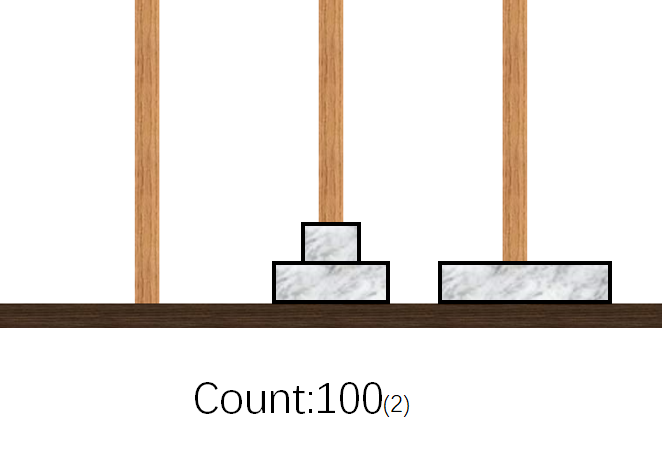
- 挪动$1$号盘到$A$柱
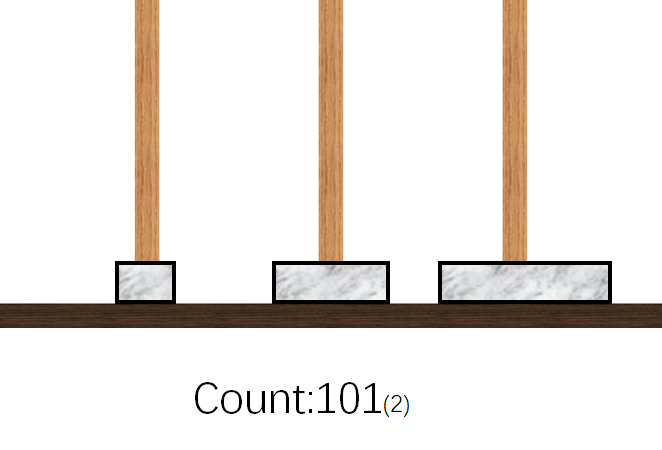
- 挪动$2$号盘到$C$柱
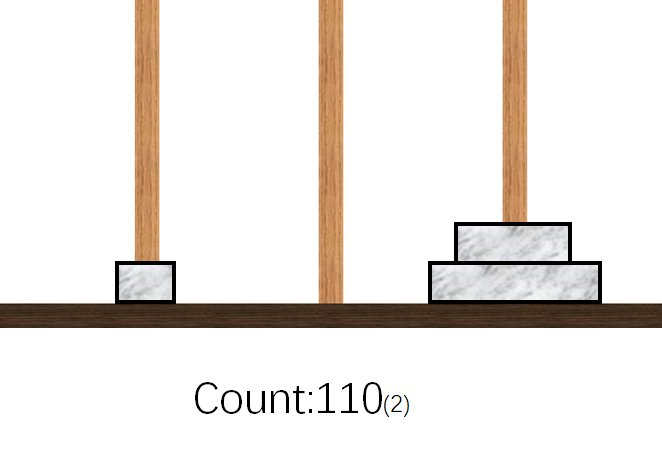
- 挪动$1$号盘到$C$柱
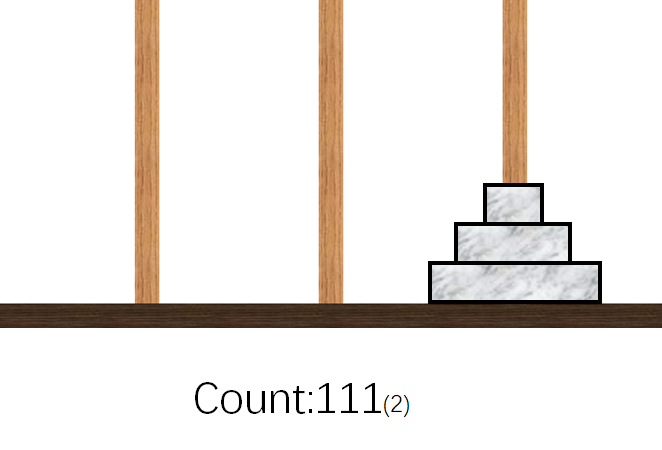
- $The$ $End$
那么,我们来看看,这跟二进制又有什么关系呢?
先看挪$1$号盘时出现的变化:

怎样?是不是发现了什么?
没错!就是说:当$lowbit(cnt)=10_{(2)}$时,即第二位为1时,下一次就要挪动$1$号盘。
再具体一点,我们甚至可以知道怎么挪一号盘
因为$1$号盘是最小的,所以他挪动时可以任意摆放,也就是说你可以挪动到剩余两个柱子中的任意一个上
但最优解法只有一种,那么我们回过头去看1是怎么挪的:
我们发现:
它的轨迹是$A$->$C$->$B$->$A$->$C$
这说明:它其实一直在向左挪动
只不过到$A$时把$C$视作左柱而已。
惊人的结论$1$
- 当$lowbit(cnt)=10_{(2)}$时,即第二位为1时,我们把$1$盘向左移动,其移动方向为$C->B->A->C$的一个环路径。
那我们继续,看盘$2$的移动:

我们发现,二号盘总是被迫挪动到唯一的能挪动到的盘。
继而发现$2-n$号盘具有同一特性:总是被迫挪动到唯一的能挪动到的盘。
好了!现在我们可以进行非递归的解决了!
$move(cnt)_ {\ \ \ \ \ (\ cnt\mod\ 2\ =\ 1)} =\begin{cases}to\ \ left\ \ stick&(\ cnt\mod\ 2\ =\ 1) \to\ \ empty\ \ stick&(\ cnt\mod\ 2\ =\ 0)\end{cases}$
当然,细心的同学可能发现了:为什么$move$函数会有一个$(\ cnt\mod\ 2\ =\ 1)$的条件呢?
- 我们来看一看:
我们讨论过$3$个盘的情况,再来讨论$4$个盘。
显然,我们由递推的思想得到,只要把$1-3$盘按照刚刚的思想挪到$C$柱,再把$4$盘挪到$B$柱,再用与之前按相同的步数挪到$4$的上面就好了。
是不是有什么不对?
是的!!我们成功地把四个盘子挪到了$B$柱上,而不是$C$柱!
- 怎么办?
当然是改变策略:每次把最小的盘$1$向右挪
这样,我们由递推得到把$3$个盘子转移到了$B$上,接下来我们只要把$4$盘挪到$C$柱,再把三个盘挪到$4$盘的上方即可,这样是满足条件的。
- 那么我们再写一个式子:
$move(cnt)_ {\ \ \ \ \ (\ cnt\mod\ 2\ =\ 0)} =\begin{cases}to\ \ right\ \ stick&(\ cnt\mod\ 2\ =\ 1) \to\ \ empty\ \ stick&(\ cnt\mod\ 2\ =\ 0)\end{cases}$
- 二进制的解决方法到这里就结束了,那么为什么呢?
还是递归
- 我们看二进制是如何进位的:
我们假设第$k$位发生$0->1$的更新即此盘的移动,那么我们要移动第$m$个盘,就一定要把二进制数$cnt$的第$m$位前面的所有位都更新为$0$并向$m$位进位。
- 想起什么没有?
我们在挪动汉诺塔时,挪动从上到下第$m$个盘时,要把它上面的所有$m-1$个盘都挪走!那么就是要把前面$m-1$位的$1$全部进位。
原理也解释完毕了,想必大家也理解了,下面有一个$6$盘汉诺塔,大家可以手动试试看。

| 步骤 |
|---|
| 1.$000001$ |
| 2.$000010$ |
| 3.$000011$ |
| 4.$000100$ |
| 5.$000101$ |
| 6.$000110$ |
| 7.$000111$ |
| …… |