1.对于SBT树高log n的证明
设 f[x] 是高度为 x 的结点个数最少的 SBT 的结点个数。
f[x]有一个结论如下:
$\sf f[x]=\begin{cases}1,(x=0)\2,(x=1)\f[x-1]+f[x-2]+1,(x>1)\end{cases}$
显然,f[0]=1,f[1]=2;
f[x]=f[x-1]+f[x-2]+1(x>1)的证明:
对于每个x,设 t 指向一个高度为 x 的 SBT ,然后这个 SBT 包含一个高度为 x-1 的子树。不妨设它就是左子树。
通过前面对于 f[x] 的定义,我们得到t[ls(x)].siz>=f[x-1],并且在左子树上有一棵高为 x-2 的子树,或者说有一棵大小( siz )至少为 f[x-1] 的子树在左子树上。由性质可得t[ls(x)].siz>=f[x-2]。
故而有f[x]=f[x-1]+f[x-2]+1(x>1)。
也可以通过构造特殊SBT进行证明:
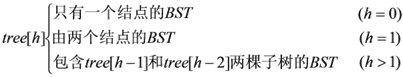
对于递推函数f,我们发现它具有斐波那契数列的相似性质,则利用特征根方程可以求出通项公式:
$\sf\Large f[x]=\frac{u^{x+3}-v^{x+3}}{\sqrt5}-1=||\frac{u^{x+3}}{\sqrt 5}-1||$
其中u=$\frac{1+\sqrt{5}}{2}$,v=$\frac{1-\sqrt{5}}{2}$。
下面是一张计算表,可以看见f[x]较小的值
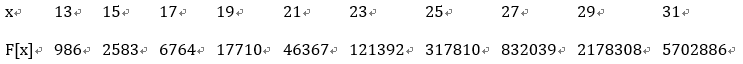
那么接下来对于最差高度maxh进行证明(引自论文):
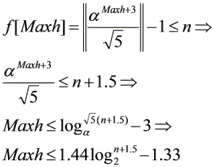
可得最差树高是log n级别的。
2.对于SBT maintain()时间复杂度O(1)的证明
通过前面的结论,我们可以很容易的证明 Maintain 过程是非常有效的 过程 。
评价一棵 BST 时有一个非常重要的值,那就是 结点的平均深度。它是通过所有结点深度和除以总结点个数 n 获得的。通常它会很小,而 BST 会更小 。
因为对于每个常数 n ,我们都期望结点深度和 (缩写为 SD ) 尽可能的小。
现在我们的目的是削减结点深度和,而它就是用来约束 Maintain 的次数。
回顾一下 Maintain 中执行旋转的条件,会发现结点深度和在旋转后总是在减小。
感性分析后,再进行理性证明(引自论文):

可见maintain()函数均摊只有O(1),非常快速。
3.SBT综合性能分析
一张图说明效率:
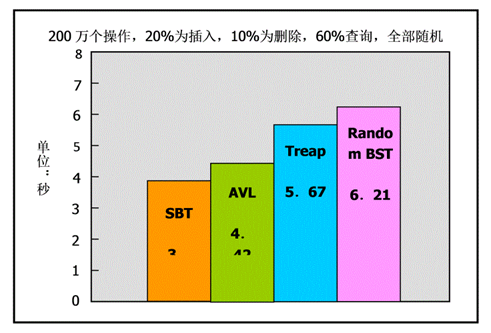
两张表对比速度:
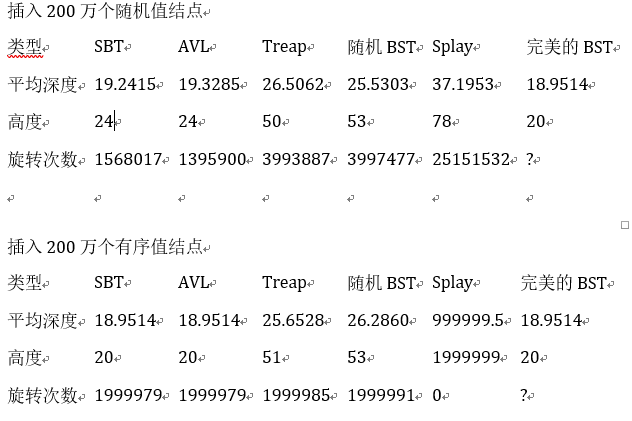
这说明SBT在时间复杂度上胜于一般的平衡树。
另外,不像一般平衡树,SBT只用维护一个额外的siz值即可,而siz值往往又是题目中要求的,所以可以视作不存储额外信息。而treap等则需要另外存储随机权值,颜色等等,空间上SBT也略胜一筹。