$\tiny\text{似乎巨佬都没有翻译题目,其实部分难度在于题目翻译,所以:}$
先翻译下本题的题意:
- $n$个点,$n-1$条边,任意两点可以互相到达,每条道路仅从属于一条“赛道”。
眼熟?$\color{blue}\text{其实就是一棵树。}$
对了!$\color{red}\text{就是二分答案!}$
那么整道题翻译出来就很简洁了:
- 给出有$n$个节点的一棵树的信息,从中选出$m$条链,满足链之间互不相交,并最大化最短链长。
进入二分前,先想想二分什么,二分所需要的上界在哪。
那么我们可以树形$DP$一次求出树的直径。
比如我们拿$Sample\ 2$来讲:($len$是边长)
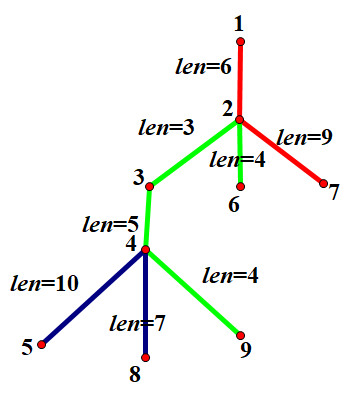
那么我们可以看到,这棵树被切成了$3$条无交集的链,其中最短链是$1->2->7$,它的长度是$15$,此时最大化。
这棵树的直径是$7->2->3->4->5$长度为$27$,那么二分最短边的长度就好了。
回到这幅图,我们可以看到对于每条链,我们可以找到其上一个点(以下简称特征点),使得此链与该点的上方树无交集。即是说,该链为特征点子树的子集。
那么对于上图,特征点分别为(按颜色):$\color{red}\text{1}$,$\color{lime}\text{2}$,$\color{darkblue}\text{4}$
下面是废话时间:
如果一个链,它经过了结点$i$的父结点,同时包含了$i$到子结点的某条边,那么它只能包含$i$到所有子结点的边当中的一条。
这句废话推广一下的话就很有用了:
对于任意节点$i$及其子节点$j,k$以及其中的一条链$i->j$,有$3$种情况需要讨论:(设$i$的父结点为$f_i$)
那么分类就很简单了:
对于每个结点$i$进行连边的尝试(连一个或两个):
如果连一个的话就把新边长向上传递并与父结点合并入同一链(连两个的话说明它就是特征点)
似乎思路走远了?不是要二分吗?
再看看?我们有一个二分链长$len$,就可以按照上面的步骤连了,如果连出来的链长大于$len$就计数重开一条新链,如果统计下来链数不够,我们就缩小$len$二分,反之类比。
似乎忘了什么?我们不仅要保证链的数量最多,还要保证最短的链最大化!那么我们每次传回父结点的边长一定要尽量长。
所以我们就有加链条件:
$len_pre+len_now>=binary_len$
这里采用$multiset$进行维护。
复杂度?不好说
下面是代码,有简洁的注释,又不懂的欢迎在评论区提问,即时$Update!$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
| #include <bits/stdc++.h>
#define ri register int
using namespace std;
int read()
{
int num=0;
int flg=1;
char c=getchar();
while(!isdigit(c))
{
if(c=='-')
{
flg=-1;
}
c=getchar();
}
while(isdigit(c))
{
num=(num<<1)+(num<<3)+(c^48);
c=getchar();
}
return num*flg;
}
const int maxn=20031125;
int n,m;
struct edge
{
int to;
int nex;
int val;
} e[maxn<<1];
int head[maxn];
int edge_cnt;
void add(int u,int v,int val)
{
e[++edge_cnt].to=v;
e[edge_cnt].nex=head[u];
e[edge_cnt].val=val;
head[u]=edge_cnt;
}
bool vis[maxn];
int dia,dp[maxn];
void diameter(int u)
{
vis[u]=true;
for(ri i=head[u];i;i=e[i].nex)
{
int to=e[i].to;
int val=e[i].val;
if (vis[to])
{
continue;
}
diameter(to);
dia=max(dia,dp[u]+dp[to]+val);
dp[u]=max(dp[u],dp[to]+val);
}
}
struct node
{
int cnt,edge;
node(int cnt_,int edge_)
{
cnt=cnt_;
edge=edge_;
}
};
int flg;
node dfs(int x,int fa,int binary_len)
{
int cnt=0,edge=0;
multiset<int> _set;
for(ri i=head[x];i;i=e[i].nex)
{
int to=e[i].to;
int val=e[i].val;
if (to == fa)
{
continue;
}
node son=dfs(to,x,binary_len);
if (val+son.edge >= binary_len)
{
++cnt;
}
else
{
_set.insert(val+son.edge);
}
cnt += son.cnt;
}
while (!_set.empty())
{
multiset<int>::iterator it=_set.upper_bound(0);
int top=*it;
_set.erase(it);
it=_set.lower_bound(binary_len-top);
if (it == _set.end())
{
edge=top;
}
else
{
_set.erase(it);
++cnt;
}
}
if (cnt >= m)
{
flg=true;
}
return node(cnt,edge);
}
int ans;
int main()
{
srand((time)(0));
n=read();
m=read();
for(ri i=1; i <= n-1; i++)
{
int u=read();
int v=read();
int val=read();
add(u,v,val);
add(v,u,val);
}
diameter(1);
int l=0;
int r=dia;
int mid;
while (l<=r)
{
mid=(l+r)>>1;
flg=false;
dfs(1,0,mid);
if (flg)
{
l=mid+rand()%2;
ans=mid;
}
else
{
r=mid-rand()%2;
}
}
return 0&printf("%d",ans);
}
|
反思与小结:(前面浪费时间系列)
其实根本不需要求直径,无脑取一个大值就好了(所有边长之和就不错),求直径的时间可以用来多二分几次,并且此题时间卡得并不很紧,否则必须要用平衡树维护链长和特征点了。
