0%

题解-LG3099

发表于 更新于 分类于
一道卡了我半年的计算几何，统计凸包内点数

本题题意简单：给出两组大小为n的点集，问点集A中任取三点形成的三角形围住点集B中点的数量，以及B包A的数量。

其实题目可以进一步简化：我们来看一幅图（样例解释）

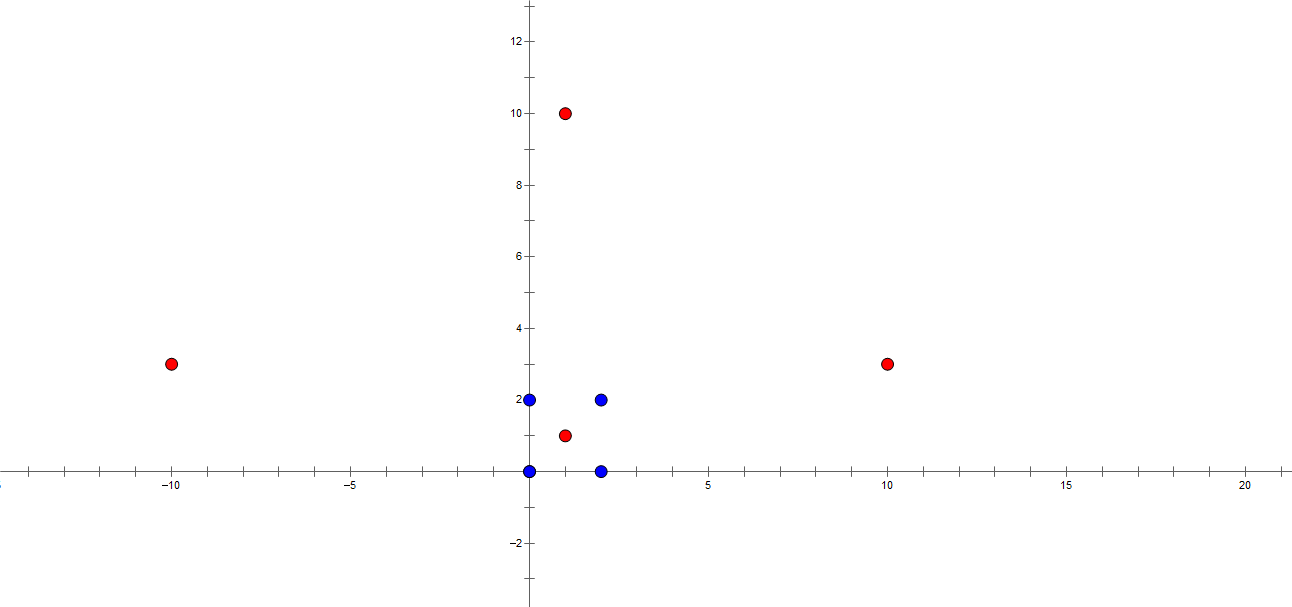
我们可以主观感受一下，红点被蓝点包了一个，蓝点被红点包了俩。

回想一下，我们是怎么判断的呢？一个个三角形枚举吗？$\sf\color{red}\text{并不是！}$

多感受几次，我们发现：如果一个点被异色点围成的一个多边形围住，那么它就被捕了（如下图）。但是为什么？

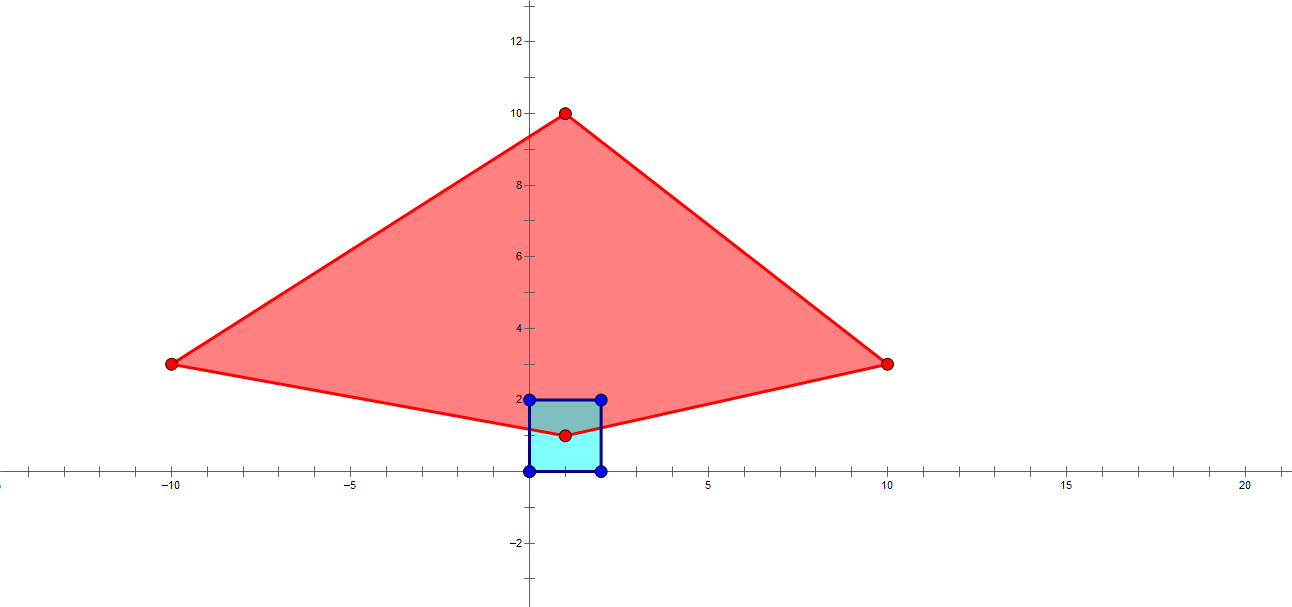
别忘了，当你把所有可能的三角形围出来的时候，就注定把这些点围成的多边形覆盖，因为所有的三角形边中一定包含了这个多边形的边。还是以图举例。

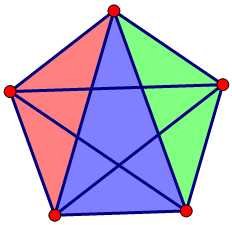
显然这个五个点围出了五边形（为了美观，有部分三角形未画出）

直入主题，这样的多边形我们称之为$\sf\color{red}\text{凸包}$。那么我们现在需要的就是判断点是否在凸包内了。

关于凸包，网上已有详细的讲解，此处不作赘述。

那么此题中，我们采用的是常规的二分判断叉积法判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
//取其中的一个点，他和其他点可以组成n-2个三角形，利用二分判断差积，
//判断他是在当前三角形内，还是在三角形左边，还是在三角形右边，或者是三角形外。
int check(dot b,int n)
{
	int l=1;
	int r=n-2;
	while(l<=r)
	{
		int mid=(l+r)>>1;
		ll cr1=(bor[mid]-bor[0])*(b-bor[0]);
		ll cr2=(bor[mid+1]-bor[0])*(b-bor[0]);//叉积
		if(cr1>=0&&cr2<=0)//也就是说此时该点b在bor[mid]上方或其线上，又在bor[mid+1]下方或其线上
		{
			if((bor[mid+1]-bor[mid])*(b-bor[mid])>0) //bor[mid]->bor[mid+1] 与 bor[mid]->b 的叉积
			{
				return true;
			}//如果此时叉积大于等于0,说明该点b在该三角形内部或者边界上
			//经过卡数据，此题边界点不计入内。
			return false;//点在三角形外部
		}
		else if(cr1<0)  //如果该点在bor[mid]下方，那么把上边界缩小到mid-1
		{
			r=mid-1;
		}
		else //如果该点在bor[mid+1]上方，那么把下边界拉至mid+1
		{
			l=mid+1;
		}
	}
	return false;
}

那么有了判断法，我们就先求出AB两点集的凸包，并且用对集的点一个个代入判断即可，这是思维量最小的方式。

  • 不得不提的一点：此题的边界不算入内，有一个点恰好点在凸包边界上，不能计入内。

为不影响阅读，完整代码请移步此处