0.Brief Intro
随机化算法在我们日常做题当中的应用可谓是少之又少,如遇LuoGu1337这样的题目,我们往往不会考虑模拟退火,而是去考虑半平面切割凸包这样正常的解法。
但随机化在日常生活中应用广泛:从决定命运的$\sf \text{掷骰子}$到较为复杂而高效的$\sf \text{Pollard\ Rho因数分解算法}$,随处可见随机化的身影。
1.First impression
恰如其名,随机化就是一种特殊的暴力,打个比方:
假如你要做一篇阅读题,普通暴力是逐字逐句读找到答案,随机化是一目十行寻找答案。
我在做阅读题时使用的是第二种方法,只不过随机范围较小。这种方法的利弊就不必多言:
利:对于某些有序数据(好比是含有一段无用文字的文章),随机化能够概率跳过不看,从而更快地找到答案。
弊:对于差异很大的数据(好比是字字珠玑的一段),随机化可能浅尝辄止。
至于百科上则是这样描述它的:
只是由于随机化算法比较难于掌控,所以并不是很多人都接触过。
随机化算法是一个很好的概率算法,但是它并不能保证正确。
这两句话就好像在说:你人很好,但你是个好人。
随机化真的如此危险?竞赛中宁可暴力也不随机?抬头看标题:$\Large\sf\text{随机化美学}$
2.随机化算法串讲
显然,随机化的应用并不罕见,如果要我列出一个算法的集子来,我会说:I can do this all day.接下来将对随机化算法进行讲解(非难度排序)
1°是非状态随机化
所谓是非状态,就是说类似背包内的取与不取两种状态,不是取就是不取。显然,最原始暴力,我们只要对每个物体枚举2种可能,那么最差(全放下)也就$\Large{2^n}$种可能性而已。
先不讨论背包的正解(无价值),我们来拿另一个例子想想如何随机化。(背包的随机化稍后与模拟退火同讲)
另:此题详细题解在我的另一文章
1 | 给一个数列和m,在数列任选若干个数,使得他们的和对m取模后最大 |
我们发现,这种序列选数求某个最值的题目往往可以随机拿分。
我们可以随机每个数选或者不选,并且如法炮制数万甚至数十万次并且不断与之前最值打擂台,在数十万次尝试下最值出现的概率很高。
针对此题,我们可以随机两回,随机选多少个数,随机每次选哪个数,再加个$vis[]$记录下是否使用就行。
如果看过我的题解,你可能会惊叹于$for()$循环的常数:50000!这就是是非状态随机化的一大特点:多试几次。
你不必担心跑得慢,因为正解那边折半搜索也是指数级的,稳妥为上。
总结一下,是非状态随机化适用于$\large\sf\text{数据大 时间不紧 对象状态少 要求输出“统计数据”}$的题目(可以看出,它并不只适用于仅有是非状态的题),而此时的正解有可能也较慢。
2°爬山算法
严格意义上来讲,爬山算法的随机化过程很少。此处提到它仅仅是为了下方的模拟退火做铺垫。
看名字,这个算法的最基础应用就是求函数极值,即从当前点开始,每个点的值与相邻点的值比较,把指针挪至接近极值的那一个。
扔个图解,图片来源于网络。
3°模拟退火
概念此处仅简单讲解。如需详解请下楼右转
1 | 模拟退火(SA) |
上面那块太长,换一个说法:
1 | 模拟退火就是进行多次循环,每次循环会以一个与当前答案正确度相关联的概率跳出当前域的算法。 |
模拟退火的应用可谓是远在天边,近在眼前,你想用它时仿佛处处都是它,关键时刻你又常常想不到它。
作为一个随机化算法,模拟退火优于一般的随机,因为它不仅仅是像取随机数那样真正意义上的随机,而是在降温的过程中逐渐逼近答案,并且偶尔地出界探索更优解。
模拟退火比爬山就优秀在这里,模拟退火在温度较高时跳动概率大,而温度低时(逼近正解)跳动概率小。
因此模拟退火很大程度上改良了爬山算法会卡在一个小峰的尴尬弱点,也同时比乱序随机来得更准。
退火能够应用的范围很广。下至装箱问题这样的01背包,上至Haywire这样的难题(貌似没有平衡点难),都能见到它的身影,甚至在严谨的省选赛中SA也能占有一席之地(四川、江苏、河南、天津,etc)。
最后简单讲解一下模拟退火的实现,就以下图的求极值为例。

第一步,定初温$\mathcal T$,不能太低($1000^+$)。
第二步,定降温系数$\Delta$,一般在0.997,有些题粗放到0.92也行。
第三步,利用metro_polis接受准则产生当前温度能接受的随机值。
- 关于metro_polis接受准则
若在温度T,当前状态i → 新状态j
若Ej<Ei,则接受 j 为当前状态
否则,若概率 p大于[0,1)区间的随机数,则仍接受状态j为当前状态;若不成立,则保留状态i为当前状态。
这个概率p的产生又是随机化的一大美学了:exp的巧用。
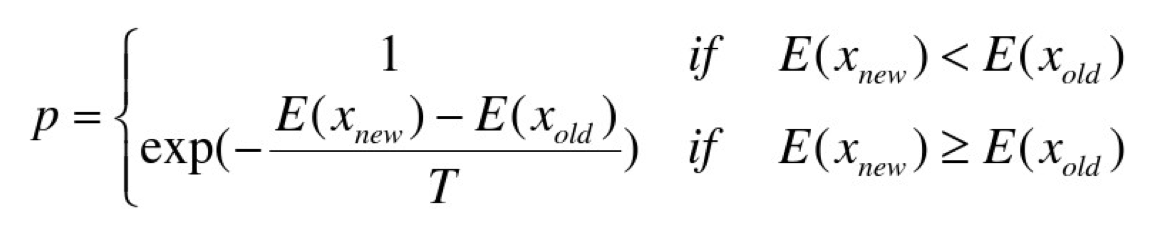
图中我们可以看出,温度越高则跳出概率越高,温度越低则p也越低,即p与T正相关,且这个函数的值总是在[0,1)内,也就是说我们在这个区间内随便取数,比p小的概率就是p所代表的概率。
4°数论中的随机化
判断素数一直是数论界的热门话题之一,如何高效地查找因数也是人们热衷的研究。
1)从费马小定理说起
费马小定理
对于质数p和整数a,有$a^p$ ≡ a(mod p)。
这个结论大概率可以视作反之亦然(几乎充要)。
反推有$a^{p-1}$ ≡ 1(mod p)
由上式我们可以得到费马测试的方案:
随机取多个整数a,对p进行同余测试,如果均通过则为质数。
但费马测试还是有小概率出错的,如下式
$2^{340}\ mod\ 341=1$显然成立
然而341是合数!对于341这样奇怪的反例,我们称为伪素数。
据研究,在1e12范围内共有5597个伪素数,这可不是小概率事件(出错率在0.00011,引自Matirx67的blog)。
2)Miller&Rabin
在发现这个bug以后,Miller和Rabin二人为费马测试的bug打上了补丁:二次探测定理
按照上述,费马测试需要更换多个a,而二次探测定理则换了一个角度检查。
如果p是奇素数,则 $x^2 ≡ 1(mod\ p)$的解为 $x ≡ 1$ 或 $x ≡ p - 1(mod\ p)$
——二次探测定理
那么我们来手动模拟一下M_R的做法:
$I.$得到$a^{n-1} ≡ 1 (mod\ n)$
$II.$看指数n-1是否为偶,若为偶,则将其指数折半,用二次探测定理检查。
那我们回头看看上面的那组卡掉费马测试的数据:
$2^{340}\ mod\ 341=1$
我们得到式子后进行如下的操作:
$2^{170}\ mod\ 341=1$二次探测也被突破?
那么再进行一次呢?
$2^{85}\ mod\ 341=32$
显然,341在第二次的二次探测定理下被排除。可见M_R也具有出错率,但可以通过多次探测缩小错误率。
- 研究发现,M_R素数检测n次的错误率仅有($\frac{1}{4}$)$^n$,所以多来几次就好。
3)$\sf\rm\ Pollard_\Large\rho$(科普向)
Pollard_rho,是当今最为优秀的随机化分解因数算法,由于其高效且随机,其模板是黑题,OI界也几乎用不到如此高效却复杂的因数分解算法。
下面简单介绍一下$\rho$的算法流程。
1 | 第一步,先判断给出的数是否为素数。 |
具体地,我们不会单纯地寻找一个数的因数,而是利用上了随机化的加持。
对于数n,假设要找的因数为t,我们先随机取一个$x_1$,再构造$x_2$,使条件$t|(x1-x2)$成立,并且条件$(x_1-x_2)|n$不成立(|:整除)。
此时有一个结论:若$gcd(x_1-x_2,n)$不为1,则该值为t。
如果值为1,则调整$x_2$使其再次符合条件(调整方式可以为$x_2=x_2*x_2+\phi$)(其中的$\phi$为随机值)。我们在调整的过程中如果出现了$x_1=x_2$的情况,则说明$x_1$选取不当,须重新选$x_1$。
pollard发现,在调整$x_1$的过程中,$x_1$与$x_2$最终会形成$\huge\rho$循环。
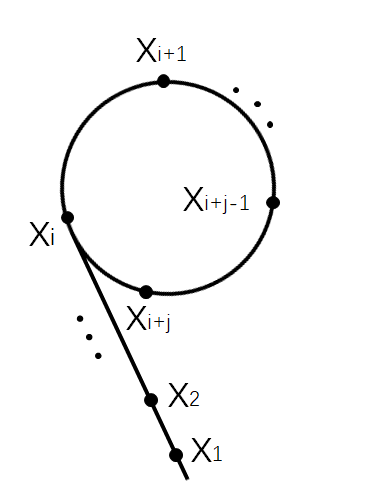
计算出因数后只需要判断下是否为质数就行了,此处就要引进上文的M_R判素法了。
5°随机化的其他运用
随机化在很多不起眼的地方也起着巨大的作用,看上去傻乎乎的决策却也有着猴子打字写出成书的可能。
或许随机化不能称为优化,有人甚至认为它是劣化,但不得不说的一点是:没有人能卡掉随机优化,除了坏运气。
1)spfa?
众所周知,spfa有个双端队列优化,那么到底把新来的点放队头还是队尾呢?rand()%2就是这样的01决策的利器。
2)排序?
真的,真的请各位不要再嘲笑random_shuffle了
——fst
什么?比$O(NlogN)$更猛?(应该不会快过桶排)
对于随机化排序,我只能说:这是可能发生的。
因为对于一串相当有序的序列,随机化的效率还是很出色的。
引用平凡的幸福的一次测试结果,
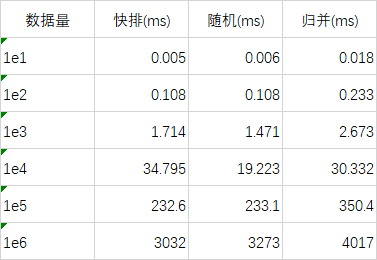
此处的所有数据均为随机产生,不具有有序性。
- 经在下测试,对于1e5的较有序数据,随机排序的效率最高可达快排的1.2倍!
3.一些细节
随机化的时候,一定要考虑好数据的大小,如果能够估计出正解复杂度更好(谁会知道正解还写随机QwQ),如果正解是搜索一类的较暴力的算法,且具有01决策性或是一些别致的可随机的提示,则可以用随机化加以解决。
随机化很重要的一点是:循环的次数一定要多,在上面的例子中,我们可以发现一个较为稳定的随机化算法一定是有一定准则的,并且往往需要多次取优处理。
在省选以下的比赛中,尽量不要考虑使用随机化,因为随机严格意义上不属于考纲。
随机化程序好写,但是千万不能让随机成为定式,它永远只是备胎,一定要有十分把握(无论是此题爆零把握还是已知正解把握),否则随机化会用运气来压制你的分数。
4.结语
随机化很美,不是么?
它似算法,却又非算法;
它永不是正解,有时却可以爆踩std。
随机化,就像生活,你还来不及做选择,就已经被随机地剪去了通往平行宇宙的枝;
随机化,不像生活,它可以一次次地重来,直到让你满意,而这却只存在于《奇异博士》中。
随机化,像极了爱情,一次次的01决策令人昏了头,却又陶醉其中;
随机化,又不像爱情,因为生活里,没有哪一个备胎会像它那样,静静地坐在你的脑海深处——
你想与不想,它总在那里,不曾离去。
有人说,选择非儿戏。
我说,随机,美得不像儿戏,而像世界。
游戏的魅力,不正在于胜负的随机性么?有胜有负才是最美。
失败的苦痛,不正在于随机么?
毕竟胜败这种非黑即白的东西,
运气总喜欢插手。
$\Huge\mathcal T$ $\Huge\mathcal h$ $\Huge\mathcal e$ $\ $ $\ $ $\Huge\mathcal E$ $\Huge\mathcal n$ $\Huge\mathcal d$