前言
话说回来,花了一个下午把练习册上几十页排列组合的题都做了的感觉还挺良好的呐……
毕竟是前OI选手,这种题秒不掉就有点淼了QAQ.
这里留下一些零碎的思想吧。
备注
在开始以前,为了方便描述,我们先给出几个定义:
方案数用$N$表示
第i个子问题的方案数用$N_i$表示
排列,组合符号为$A$,$C$
基础
排列组合是组合数学中的基础。排列就是指从给定个数的元素中取出指定个数的元素进行排序;组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。排列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。排列组合与古典概率论关系密切。
排列: $\large\mathrm A_n^m =\frac{n!}{(n - m)!}$
组合:$\large\mathrm C_n^m = \frac{n!}{m!(n - m)!}$
加法原理:一件事有n类方法,第i类有$m_i$种方法,则方案数为:$N=m_1+m_2+…+m_n$
乘法原理:一件事必须经过n个步骤,第i步有$m_i$种方法,则方案数为:$N=m_1·m_2·…·m_n$
方法整理
插空法
插空法,主要用于解决含有“不相邻”要求的问题。主要思想分为两步:将无要求的部分进行排列,假设长为L;在序列的L+1个间隙中插入特殊元素,插入第一个时有L+1种,第二个L种,以此类推。
$P1.$有a个同学,b个老师站成一排,要求老师站位不相邻,问方案数。
第一步,使用排列公式完成同学的排列:
$N_1=A^a_a=a!$
那么我们得到了这样的同学序列:
$↓a_{i_1}↓a_{i_2}↓a_{i_3}↓……$
可以看见↓的部位是可以插入老师的,一共有a+1个
第二步,a+1个空格中插入b个老师(此处默认有解)
$N_2=(a+1)·a·(a-1)···(a+2-b)=A^b_{a+1}$
第三步,乘法原理得解
$N=N_1·N_2=A^a_a·A^b_{a+1}$
备注:有时候,插空会要求不能选取两端的空,即只有a-1个空,稍作变化即可。
捆绑法
捆绑法,主要用于解决含有“必须相邻”要求的问题。主要思想分两步:将需要相邻的部分进行“捆绑”,并内部求排列;将捆绑物视作一个物品放回原问题,求排列即可。
$P2.$有a个同学,b个老师站一排,要求所有老师站位连续,问方案数。
第一步,把所有老师做排列:
$N_1=A^b_b$
随后我们就可以把这个长为b的序列当作一个整体来操作了。
第二步,将“老师”作为一个同学和其他同学进行排列:
$N_2=A^{a+1}_{a+1}$
第三步,对于每个学生排列,对老师排列进行乘法原理:
$N=N_1·N_2=A^b_b·A^{a+1}_{a+1}$
备注:捆绑的思想运用很广泛,其实就是分治的基础:把问题拆分为两个子问题分步完成。
隔板法
隔板法,用于解决划分集合问题。其主要思想是把划分集合问题改为“插入隔板”问题,从而转化为插入法解决掉。
$P3.$有a个相同的糖,分给b个人,每个人至少有c颗糖,问方案数。
第一步,把棘手的c处理成1,即每人至少一颗。
我们可以预先给每个人都发c-1颗糖,总数减少b*(c-1)即可:
$a’=a-b·(c-1)$
第二步,观察到我们要把a’个糖分给b个人,我们进行转化性思考:
a’颗糖摆成一排,我们用b-1个隔板进行分割,则恰好可以得到b份。
于是问题就转化成了向a’-1个间隙插入b-1个隔板,组合即可:
$N=C^{b-1}_{a’-1}$
备注:上面就是要用到一百次的隔板法公式,死记也要记住。
剩余法
剩余法,利用到了正难则反的思想,即如果让我们从中选择凑数,我们可以反向思维,全选然后删数。这种方法会在目标数接近总值时极为有效。
$P4.$背包里有23个价值为5的物品,有10个价值为10的物品,物品两两不同,问取出价值200的物品的方案数。
试图正面求解,发现正面凑数过于复杂,所以考虑到剩余法。
计算出全选总值为215,我们就全部选上。
问题就转化为选出若干个物品不带,使得它们的和为15即可。
15就只有两类凑法:10+5,5+5+5。
根据加法原理:
$N=C_{23}^{3}+C_{23}^{1}·C_{10}^{1}$
备注:正难则反是一种很巧妙的思路,带在身上总是好的。
反向法
反向法,同样利用了正难则反的思想,但是上个方法中,我们是从问题本身反向的,此处所讲的方法则是从求方案数的方面反向:求不满足条件的方案数。
$P5.$从n个人中选m个人出来,问指定的p个人中至少有一人在其中的方案数。
此类问题往往可以正面解出,如本题中我们可以通过讨论这p个人是否在其中并且进行容斥求解,但是显然较为麻烦。
随后考虑到“至少有一人在其中”的否定是“没有一个人在其中”,于是可以进行反向求解:p个人都不被选中的方案数,再用总方案数作差即可。
利用组合求总方案数:
$N_1=C_n^m$
计算去掉这p个人的组合数,即条件不成立的方案数:
$N_2=C^{m}_{n-p}$
作差得解:
$N=N_1-N_2=C^m_n-C_{n-p}^m$
备注:反向法可能与正解复杂度相同,而且大概率需要结合容斥法计算,务必谨慎使用。
容斥法
容斥法,往往用于解决对于多个个体有要求,并且多个要求可能同时成立的问题。在这时,如果我们简单地对于每个独立的要求,把符合要求的方案数简单加和,会发现同时满足条件的方案被屡次计算,此处就可以用简单容斥思想解决条件交集问题。
$P6.$对n个人进行排列,其中甲和丙,乙和丙均不能相邻,问方案数
容斥法往往可以结合反向法使用,此处就是一个典型的例子:我们求解让不能相邻的相邻的方案数。
所有的方案数:
$N_1=A^n_n$
通过捆绑法,甲丙,乙丙相邻的方案数均为:
$N_2=A^2_2·A^{n-1}_{n-1}$
甲丙,乙丙同时相邻的方案数:
$N_3=2*A^{n-2}_{n-2}$
通过容斥原理,不符合的方案数为:
$N_4=N_2+N_2-N_3$
那么符合条件的方案数就是:
$N=N_1-N_4$
备注:容斥法常常是作为辅助方法进行计算,也是题目的坑点难点所在,千万注意讨论重叠条件部分的方案数。
分块假设法
分块假设法,常常用于多块染色问题,此类问题的难点在于元素之间的牵制关系往往过多,用上述方法很难求解,而枚举又容易出错。分块假设法则是将多个元素整合成一块,讨论一个块的“外交关系”,如此将多块图的块数减少,再对于每一种假设在整合块内讨论+乘法原理得解。
$P7.$现有四棱锥S-ABCD,其中ABCD为底面,用四种颜色给5个顶点分别上色,使得每条棱两端点颜色不同,问方案数。
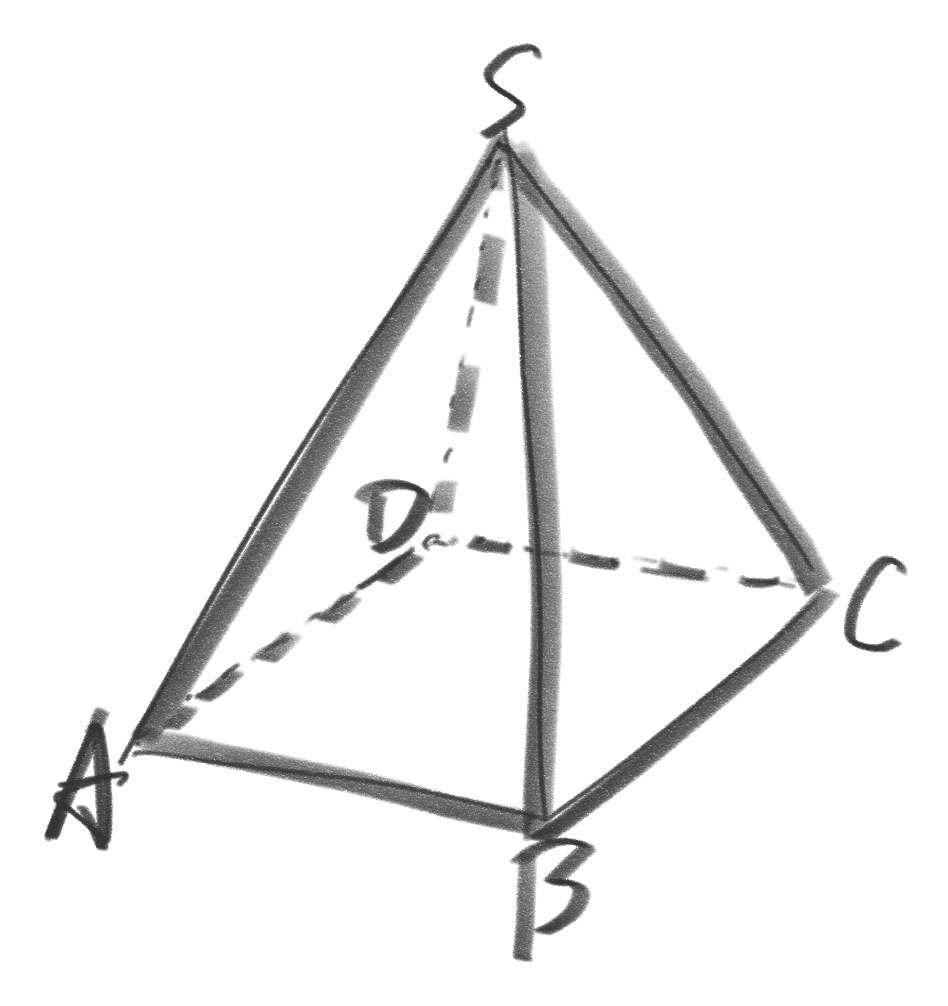
第一眼看到立体染色,我们首先想到的问题是:有没有办法降维?答案是有的。
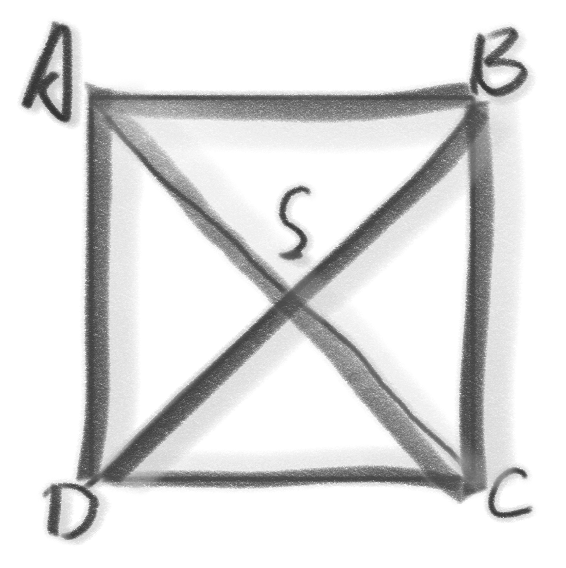
俯视图可见就是一个四分环套圆模型,把降维的图作出来:
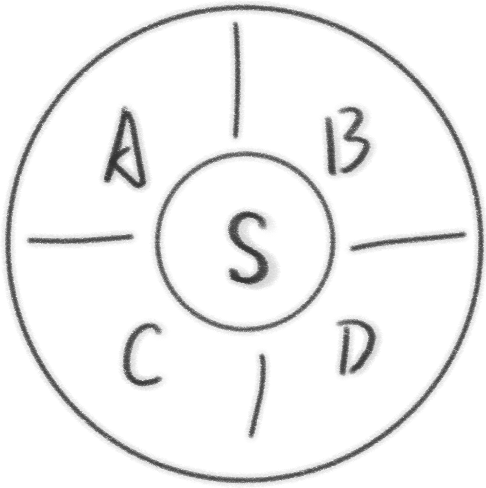
那么我们进行分块假设法解决此类问题:
第一步,将SAB分为一块,讨论该块的可能数:
$N_1=A_4^3$
第二步,对于某一种SAB讨论CD。不妨设S、A、B分别占用了1、2、3的颜色,那么若C上3的颜色,则D可以上2、4的颜色;若C上4的颜色,则D只能上2的颜色。
$N_2=2+1=3$
第三步,对于每种SAB,都有3种CD,则乘法原理:
$N=N_1·N_2=72$
备注:分块假设法可以大幅降低讨论情况数,但是在外交情况较为复杂的时候会显得难以讨论。