1.序言
听名字就知道,本文要讲的是一些圆锥曲线的结论或计算技巧,能够有效加速解题效率。
2.椭圆$\sf\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
1.对于$a$,$b$,其中较大的一个所在的那个分数的分子所代表的轴就是椭圆的长轴
2.椭圆上点的性质
- 到两焦点的距离和相等($\sf|PF_1|+|PF_2|=2a$)
- 到焦点和准线的距离比值一定($\sf\frac{\text{焦点距}}{\text{准线距}}=e$)
- 与两焦点连线的斜率之积为固定负值($\sf k_1k_2=-\frac{b^2}{a^2}$)
3.焦半径的计算
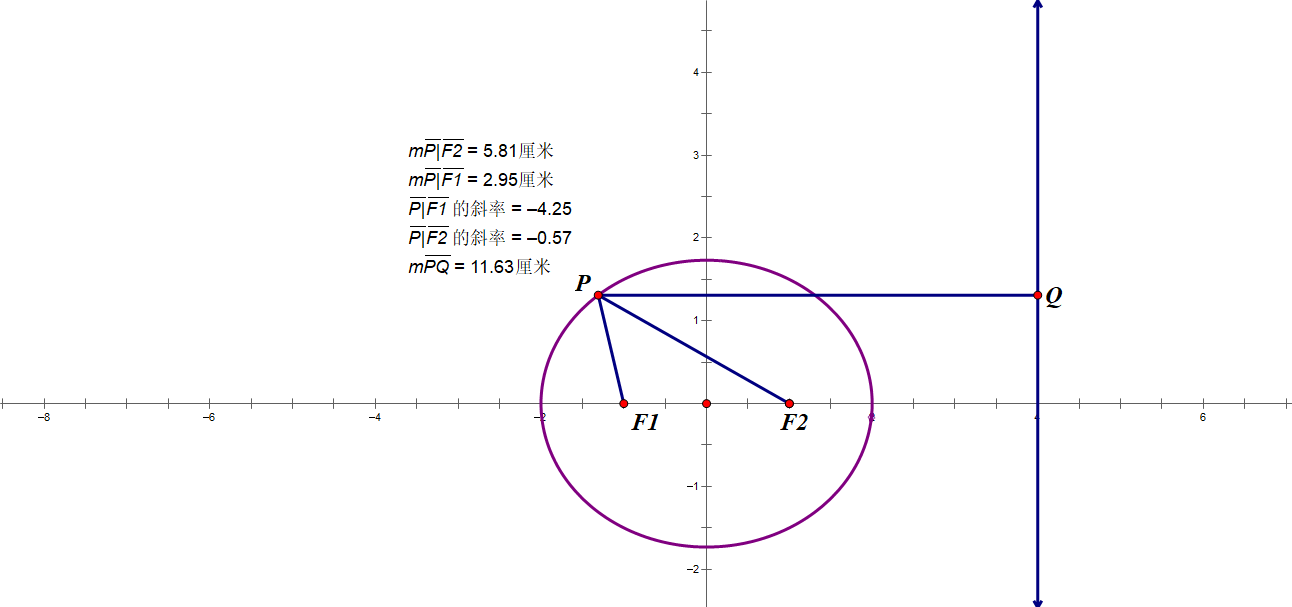
I.坐标法
$\sf|PF_\text{左}|=a+ex_0$
$\sf|PF_\text{右}|=a-ex_0$
=>两个分别以$\sf PF$为直径和长轴为直径的圆内切。

II.极坐标法
$\sf|PF|=\frac{ep}{1-e\cos{\alpha}}$
焦半径的范围:[a-c,a+c]
$\sf||PF_1|-|PF_2||\leq2c$
4.焦点弦的计算
- 坐标法:$\sf|AB|=|2a+e(x_1+x_2)|$
- 极坐标法:$\sf|AB|=\frac{2ep}{1-e^2\cos^2{\alpha}}$
其中$\sf ep=\frac{b^2}{a}$,即半通径
5.焦点弦的性质
$\sf\frac{1}{|AF|}+\frac{1}{|BF|}=\frac{2}{ep}$
以焦点弦为直径的圆与最近的准线相离
做AB在准线上的投影,以这段投影为直径的圆与AB相离
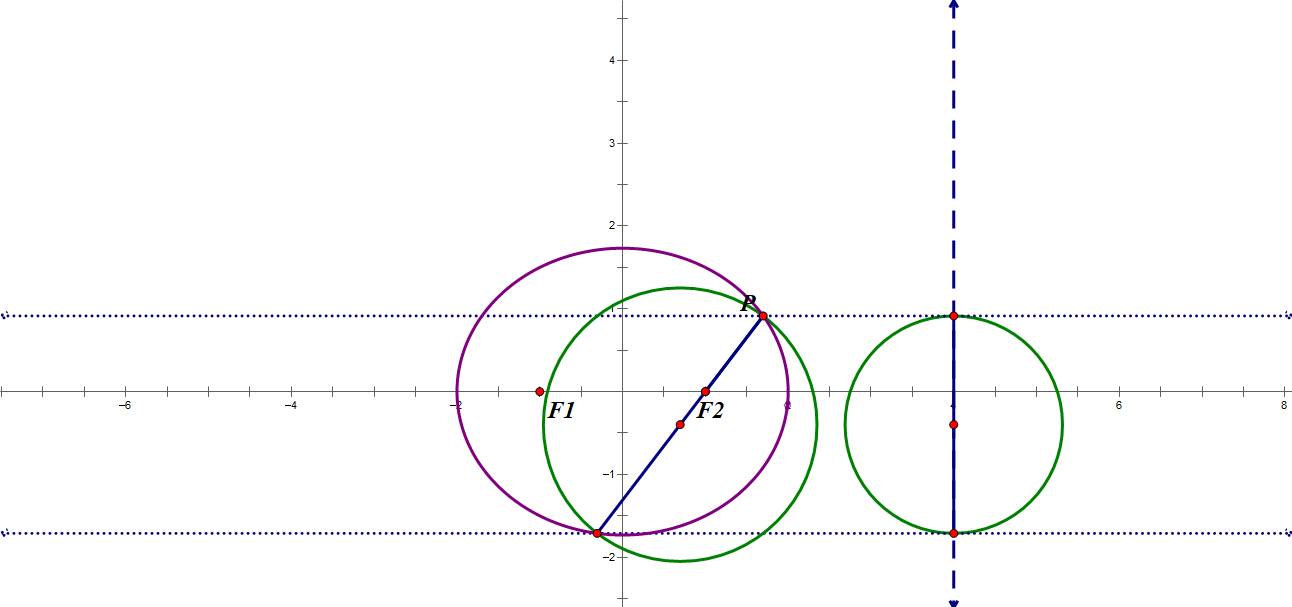
6.焦点三角形的面积
$\sf S=b^2\tan{\theta}=c*y_P$

7.弦中点性质
$\sf M=mid(A,B)$,则$\sf k_{AB}k_{OM}=-\frac{b^2}{a^2}$
8.弦长公式
$\sf\begin{cases}y=mx+n\\sf\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\end{cases}$
$\Large\sf |AB|=\sqrt{m^2+1}*\frac{\sqrt{\frac{1}{a^2}+\frac{m^2}{b^2}-\frac{n^2}{a^2b^2}}}{\frac{1}{a^2}+\frac{m^2}{b^2}}$
$\sf\begin{cases}x=my+n\\sf\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\end{cases}$
$\Large\sf |AB|=\sqrt{m^2+1}*\frac{\sqrt{\frac{m^2}{a^2}+\frac{1}{b^2}-\frac{n^2}{a^2b^2}}}{\frac{m^2}{a^2}+\frac{1}{b^2}}$
8.极点极线
- 用$x_0x$换掉$x^2$,用$y_0y$换掉$y^2$
- 用$\sf\frac{x_0+x}{2}$换掉$x$,用$\sf\frac{y_0+y}{2}$换掉$y$
即可得到极线(切点弦)
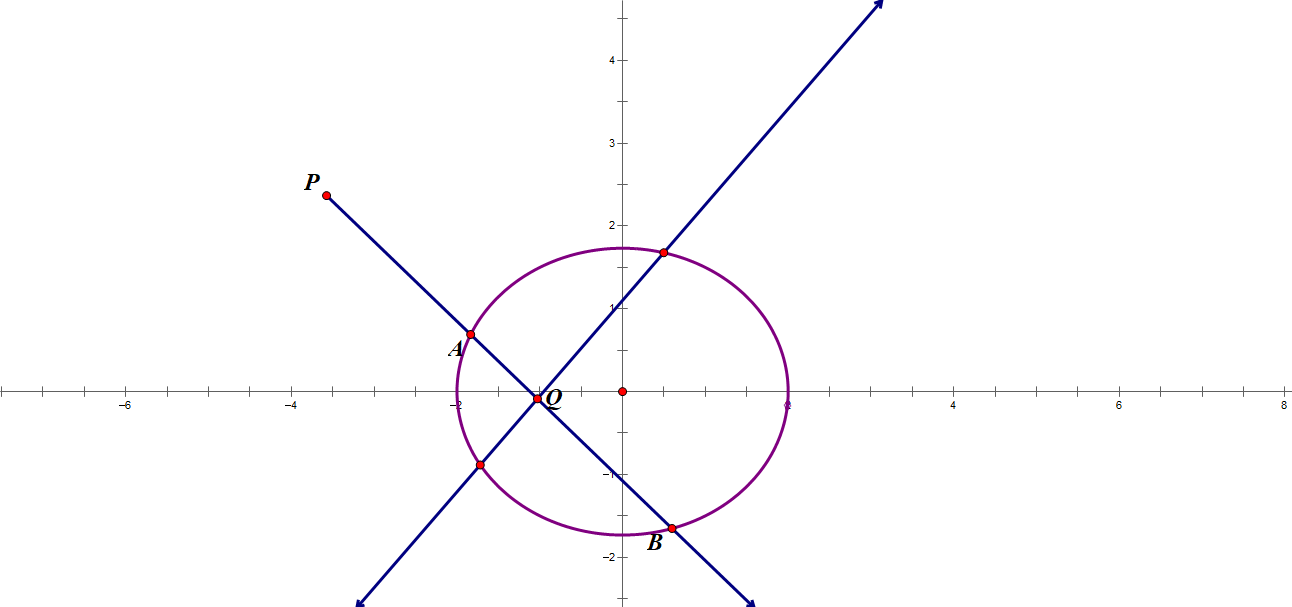
过椭圆外一点$P$做其弦$AB$,并作出其极线与$AB$交于$Q$,此时$A,B;P,Q$成调和点列。
9.焦点弦三角形的性质
待补
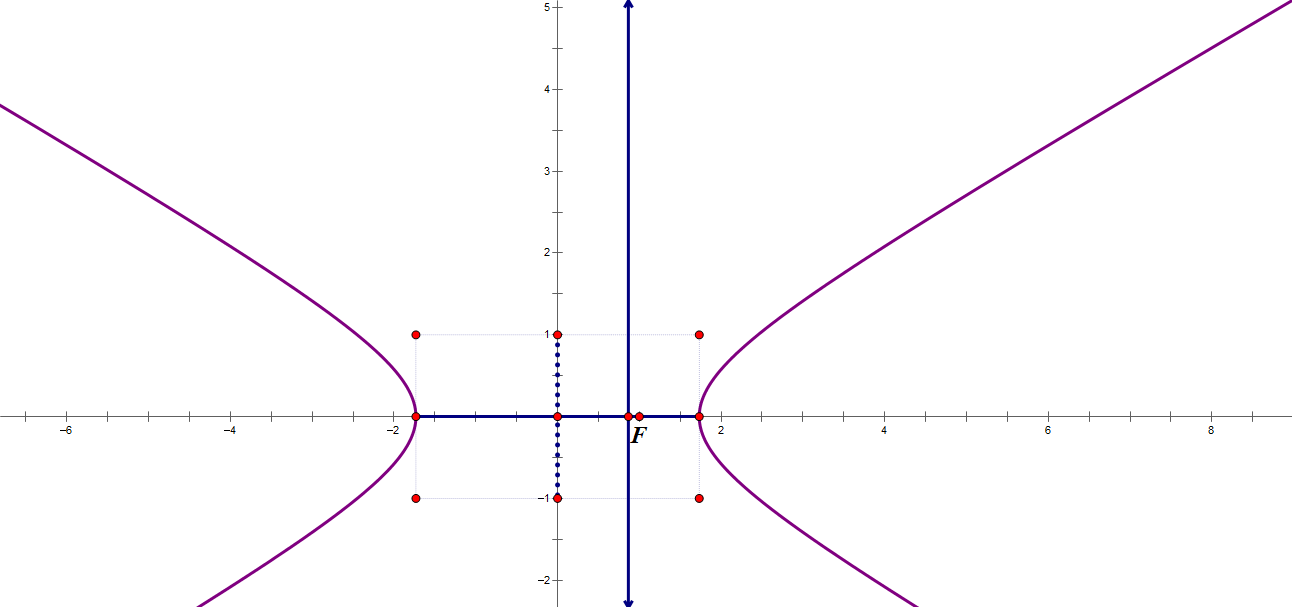
2.双曲线$\sf\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$
1.对于$a$,$b$,其中为正的一个所在的那个分数的分子所代表的轴就是双曲线的实轴
2.双曲线上点的性质
- 到两焦点的距离差的绝对值相等($\sf||PF_1|-|PF_2||=2a$)
- 到焦点和准线的距离比值一定($\sf\frac{\text{焦点距}}{\text{准线距}}=e$)
此处有$\sf a^2+b^2=c^2$